I received a picture puzzle in WhatsApp. I will explain here how I solved that using programming. I used Backtracking concept.
Received picture puzzle
below puzzle is simple algebra concept. If you have paper and pencile then it can be solved easily. But I just wanted to use some programming concept.
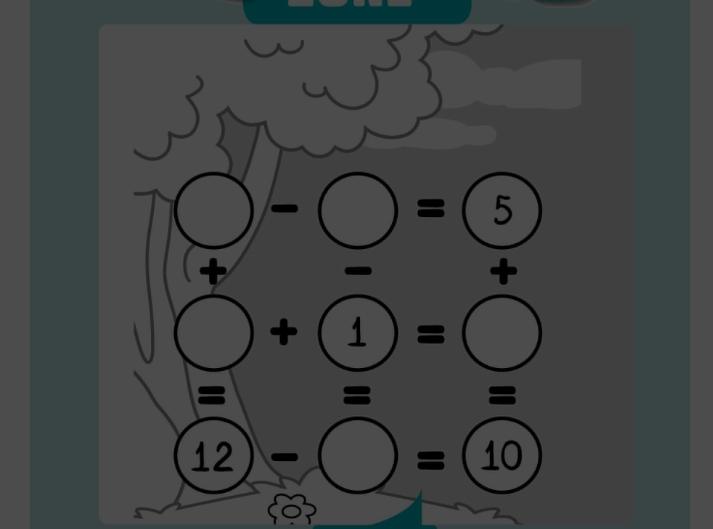
Algebra notation of the puzzle
just fill the empty circle with some letters (a,b,c,d,e)
Left to right
a - b = 5
c + 1 = d
12 - e = 10
Top to bottom
a + c = 12
b - 1 = e
5 + d = 10
Program concept
now we have the equations, just take first equation a-b=5. This is simple equation and we can easily tell that a and b can have multiple posibilities like a=10, b=5 or a=15, b=10 etc…
we will solve the above equation using backtrack. Just asign sequence of numbers and check all the possibilites.
for(let a = 0; a <= 50; a++) {
for(let b = 0; b <= 50; b++) {
}
}
Here we created two for loops with maximum values of 50. The concept here is that loop through a from 0 to 50, inside that again loop through b from 0 to 50, which means every a value will be evaluated with all b values.
so, below is the program to solve a-b=5
for(let a = 0; a <= 50; a++) {
for(let b = 0; b <= 50; b++) {
if (a - b === 5) {
console.log(`a = ${a}, b = ${b}`)
}
}
}
output of the above program
a = 5, b = 0
a = 6, b = 1
a = 7, b = 2
a = 8, b = 3
a = 9, b = 4
...
... more values here
...
a = 47, b = 42
a = 48, b = 43
a = 49, b = 44
a = 50, b = 45
Final program
we can apply the same above concept to solve the all the equations.
notation
a - b = 5 ---> 1
c + 1 = d ---> 2
12 - e = 10 ---> 3
a + c = 12 ---> 4
b - 1 = e ---> 5
5 + d = 10 ---> 6
const max = 12;
for (let a = 0; a <= max; a++) {
for (let b = 0; b <= max; b++) {
if (a - b === 5) { // <--- 1
for (let c = 0; c <= max; c++) {
if (a + c === 12) { // <--- 4
for (let d = 0; d <= max; d++) {
if (5 + d === 10 && c + 1 === d) { // <--- 6, 2
for (let e = 0; e <= max; e++) {
if (b - 1 === e && 12 - e === 10) { // <--- 5, 3
console.log(`${a} ${b} ${c} ${d} ${e}`);
}
}
}
}
}
}
}
}
}
Conclusion
Backtracking is a time consuming concept, it’s not the best solution here but let’s have fun using some program concept.